4.1. Показатели качества. Как всякая динамическая система, САУ может находиться в одном из двух режимов - стационарном (установившемся) и переходном. Стационарный режим может быть двух типов: статический и динамический. Ограничимся здесь рассмотрением лишь статического режима.
В статическом режиме, при котором все внешние воздействия и параметры системы не меняются, качество управления характеризуется точностью.
Рассмотрим САУ с двумя воздействиями: задающим Xвх(p) и возмущающим F(p). Структурная схема такой САУ приведена на рис.4.1, где обозначено: 1 - участок системы от входа до точки приложения возмущения; 2 - участок системы от точки приложения возмущения до выхода с передаточной функцией WF(p); 3 - цепь обратной связи.
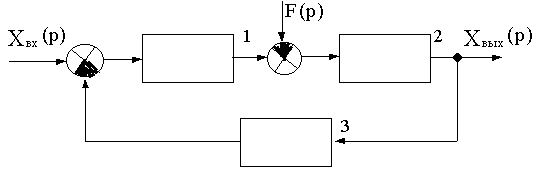Рис.4.1
В операторной форме САУ описывается уравнением динамики:
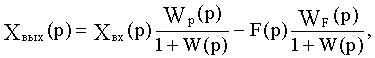
где Wp(p) - передаточная функция разомкнутой САУ,
W(p) - передаточная функция разомкнутой цепи.
Уравнение статики получается из уравнения динамики при подстановке в последнее р=0, что соответствует постоянству всех переменных, то есть равенству нулю их производных.
В рассматриваемом примере уравнение статики принимает вид:
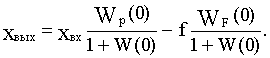
Вид W(0) и Wp(0) зависит от того, содержатся ли в системе интегрирующие звенья или нет. Рассмотрим вначале случай, когда интегрирующие звенья отсутствуют (такие САУ называются статическими).
В случае статической системы W(0)=k и WF(0)=kF так как знаменатели передаточных функций всех звеньев, входящих сомножителями в выражения W(p) и WF(p) при р=0 обращаются в единицу.
В результате получим:
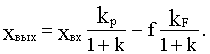
(4.1)
Статическая характеристика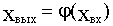 
неоднозначна из-за наличия возмущения f. Статическая ошибка 
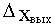при неизменном задающем воздействии определяется выражением:
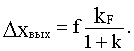
Для разомкнутой САУ уравнение статики будет иметь вид
xвых=xвхkp-fkF,
а статическая ошибка относительно замкнутой системы увеличивается в (1+k) раз:
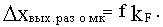
График зависимости выходной величины САУ от возмущения обычно называется внешней характеристикой, которая в общем виде представлена на рис.4.2.
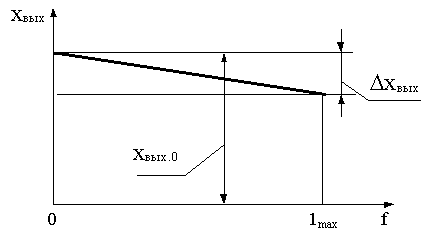Рис.4.2
В различных областях техники точность в установившемся режиме принято характеризовать величиной отклонения выходной координаты в полном диапазоне изменения возмущающего воздействия в следующем виде:
1) абсолютной величиной отклонения. Например: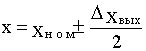 
.
Под номинальным значением xном понимается усредненное значение выходной величины;
2) относительной величиной отклонения, выраженной в процентах. Например:
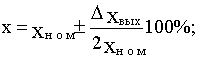(4.2)
3) статизмом внешней характеристики S, определяемым выражением
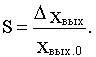
Наличие статической ошибки в общем случае является нежелательным, так как создается погрешность управления. Но для полного устранения статического отклонения требуется до бесконечности увеличивать коэффициент передачи k, что нереализуемо по ряду причин (например, по условию обеспечения устойчивости). Таким образом, в статической САУ принципиально нельзя полностью устранить статическую ошибку.
Но вместе с тем имеется путь устранения статической ошибки при конечной величине коэффициента передачи.
Введем в рассмотренную статическую САУ интегрирующее звено, причем так. чтобы оно находилось на участке 1 структурной схемы (см. рис.4.1), т.е. между точками приложения задающего и возмущающего воздействий. Теперь САУ будет описываться уравнением динамики
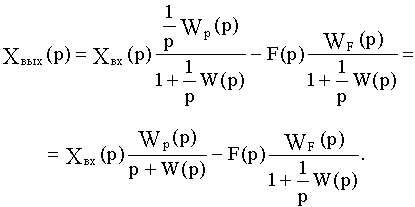
Подставив в это выражение значение р=0, получим уравнение статистики:
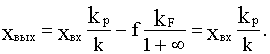
Отсюда следует, что при включении интегрирующего звена в оговоренный выше участок системы удалось полностью ликвидировать статическую ошибку, то есть получить S=0.
САУ, в которых при стремлении возмущающего воздействия к постоянной величине, отклонение выходной величины стремится к нулю и не зависит от величины приложенного воздействия, называются астатическими.
Если интегрирующее звено включить не в оговоренный выше участок структуры, а, например, в цепь обратной связи, то получим
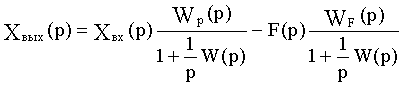
и уравнение статики
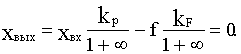
Практический смысл такая система потеряла.
В другом случае. если интегрирующее звено включить на участке 3 структуры (т.е. после точки приложения возмущения), действуя аналогично, выведем:
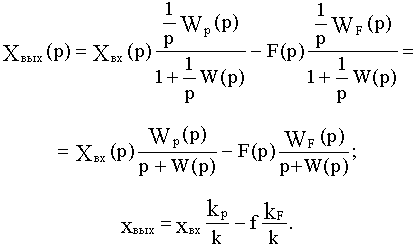
То есть система не является астатической.
Для характеристики переходного режима наибольшее распространение имеют следующие показатели качества: время переходного процесса, перерегулирование, колебательность.
Время переходного процесса характеризует быстродействие системы. Определяется как интервал времени от начала переходного процесса до момента, когда отклонение выходной величины от ее нового установившегося значения становится меньше определенной достаточно малой величины. Обычно это пять процентов.
Перерегулированием 
называется максимальное отклонение выходной величины xmax на интервале переходного процесса от установившегося после окончания переходного процесса значения xуст, выраженное в процентах:
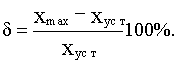
Колебательность характеризуется обычно числом колебаний переходной характеристики за время переходного процесса. В зависимости от характера затухания различают следующие типы переходных характеристик: монотонная (нет ни одного колебания); апериодическая (не более одного колебания); колебательная (несколько колебаний).
Пример 4.1
Рассчитать статическую точность системы стабилизации выходного напряжения генератора постоянного тока (см. рис.1.3) при следующих значениях параметров и воздействий: kу=0,5А/В; kп=10В/А; kд=0,1; rвн=0,1Ом; Uз=5В; Iн=(1...10)А.
Прежде всего необходимо составить уравнение статики рассматриваемой системы. Не зная передаточных функций отдельных элементов и системы в целом, составим математическое описание для установившегося режима на основе статических характеристик отдельных элементов (примем допущение, что все элементы имеют линейные статические характеристики).
В разомкнутой системе (см. рис.1.2), как было выведено в подразделе 1.2,
Uн=E-Iнrвн (а)
Э.д.с. генератора пропорциональна току возбуждения, т.е. Eг=Iвkп, где kп- коэффициент пропорциональности, зависящий от материала магнитопровода генератора, конструктивных особенностей генератора и т.д.
Ток возбуждения, в свою очередь, пропорционален входному сигналу усилителя У, т.е. Iв=Uзkу, где kу- коэффициент передачи функционального усилителя У.
С учетом этого соотношение (а) можно записать в следующем виде:
Uн=Uзkуkп-Iнrвн (б)
Уравнению (б) соответствует структурная схема, представленная на рис.4.3.
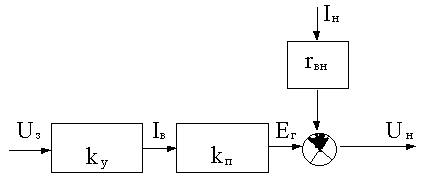Рис.4.3
В замкнутой схеме (см. рис.1.3) часть выходного напряжения сравнивается с задающим и разность этих напряжений подается на вход усилителя У, в соответствии с чем можно записать
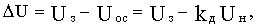(в)
где kд=R3/(R2+R3) - коэффициент передачи делителя.
С учетом формулы (в) на основе структурной схемы разомкнутой системы составим структурную схему замкнутой системы, как показано на рис.4.4.
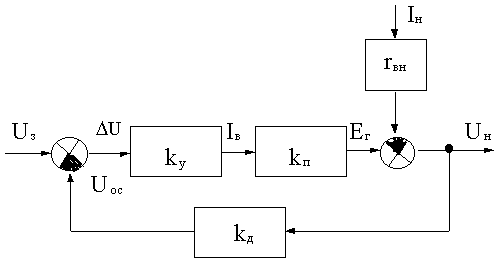Рис.4.4
С учетом правил преобразования структурных схем для схемы на рис. 4.4 получим уравнение:
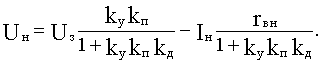(г)
Уравнение статики (г), как видим, полностью соответствует обобщенному уравнению (4.1), отличаясь лишь обозначениями.
Подставим в уравнение (г) заданные значения величин и определим максимальное UHmax и минимальное UHmin значение выходного напряжения, соответствующие соответственно минимальному (Iн=1 А) и максимальному (Iн=10 А) токам нагрузки:
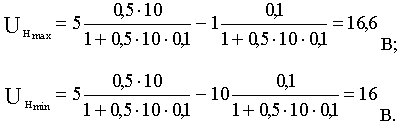
Представим выходное напряжение в форме (4.2):
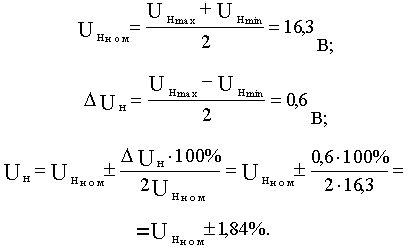
Таким образом, при изменении в оговоренномдиапазоне возмущающего воздействия (тока нагрузки) отклонение выходного напряжения не превысит величины 
1,84% от номинального значения.
4.2. Критерии качества переходного процесса
Исчерпывающее представление о качестве переходного процесса дает, естественно, сама кривая процесса. Однако при разработке САУ необходимо иметь возможность судить об основных показателях качества переходного процесса без построения их кривых, по каким-либо косвенным признакам, которые определяются более просто и, кроме того, позволяют связать показатели качества непосредственно со значениями параметров САУ. Такие косвенные признаки называются критериями качества переходного процесса.
Существуют три группы критериев качества: частотные, корневые и интегральные.
Наибольшее распространение получили частотные критерии, в основу которых положено использование частотных характеристик. Для иллюстрации возможности оценки качества переходного процесса по частотным характеристикам установим точную аналитическую зависимость между переходной характеристикой h(t) и вещественной частотной характеристикой (ВЧХ) P(
).
На основании возможности разложения функции времени в ряд Фурье единичное ступенчатое воздействие можно представить в виде выражения
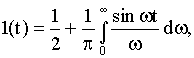
то есть суммы постоянной составляющей и бесконечного числа синусоид частотой и амплитудой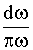 
при изменении от 0 до 
.
Уравнение АФЧХ имеет вид:
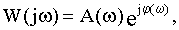
где
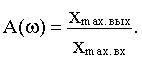
Если на вход системы подать 1(t), то каждому из входных синусоидальных колебаний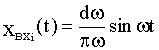 
будет соответствовать колебание на выходе [с амплитудой 
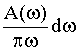, сдвинутое по фазе относительно входного колебания на угол 
(
) ]
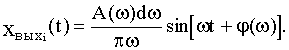
Постоянной составляющей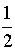 
на входе будет соответствовать постоянная составляющая 
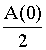на выходе.
Результирующее значение выходной величины:
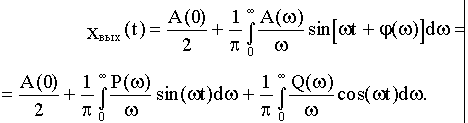
(4.3)
Так как воздействие 1(t) подается в момент t=0, то при t<0:
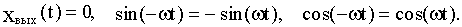
Уравнение (4.3) при подстановке значения (-t) вместо t примет вид:
(4.4)
Вычтем из уравнения (4.3) уравнение (4.4):
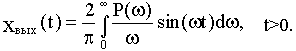
(4.5)
Пользуясь зависимостью (4.5), можно составить предварительное приближенное суждение о качестве переходной характеристики по виду ВЧХ. Различные типы ВЧХ представлены на рис.4.5.
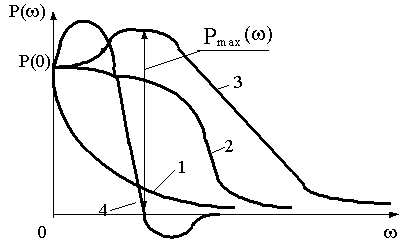Рис.4.5
Основные положения оценки качества по ВЧХ сводятся к следующему:
1) приблизительно одинаковым частотным характеристикам соответствуют приблизительно одинаковые переходные характеристики;
2) значение переходной характеристики h(t) в установившемся состоянии подчиняется следующему соотношению
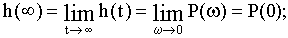
3) если ВЧХ имеет вид кривой 1 (см. рис.4.5), переходная характеристика будет монотонной;
4) для ВЧХ, имеющей вид кривой 2, характерно наличие перерегулирования у переходной характеристики величиной 
18%;
5) наличие экстремума ВЧХ (кривая 3) увеличивает колебательность до величины 
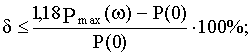
6) наличие экстремума ВЧХ в отрицательной области (кривая 4) проводит к дополнительному росту колебательности;
7) длительность переходного процесса tп оценивается приблизительно по величине интервала существенных частот cщ (в этом интервале Р() 
0,05 Р(0), причем
8) острый пик ВЧХ при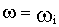 
свидетельствует о медленно затухающих колебаниях с чатотой, близкой к 
;
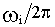9) если при некоторой частоте ВЧХ претерпевает разрыв, то САУ является неустойчивой.
Колебательность переходной характеристики можно оценить по величине относительного максимума амплитудной частотной характеристики А(), примерный вид которой представлен на рис.4.6.
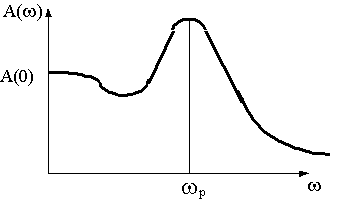Рис.4.6
Величина относительного максимума называется показателем колебательности М и определяется отношением
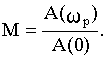
При М<1 переходная характеристика неколебательна. Чем больше М, тем больше колебательность. При М
- незатухающие колебания. Оптимальным обычно считается М=1,3-1,5. При этом переходная характеристика имеет слабую колебательность с частотой, близкой к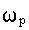 
.
Вследствие предельной простоты построения ЛАЧХ удобно пользоваться именно этой характеристикой. Информацию здесь несет среднечастотная часть характеристики. При частоте среза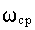 
наклон ЛАЧХ должен составлять минус 20 дБ/дек, а значение 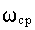определяется временем переходного процесса tп и перерегулированием :
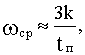
где k берется по графику на рис.4.7 в зависимости от величины .
Сопрягающие частоты ЛАЧХ слева и справа от 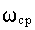, как показано на рис.4.8, рассчитываются по выражениям:
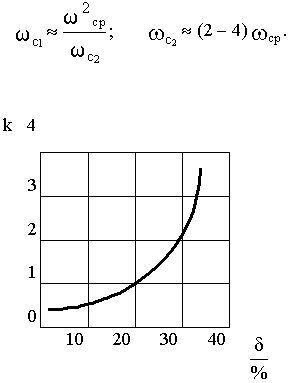
Рис.4.7
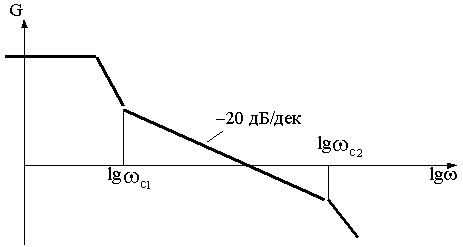
Рис.4.8
Величины наклонов ЛАЧХ слева от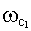 
и справа от 
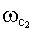на качество переходного процесса почти не влияют.
Группа корневых критериев основана на оценке качества переходного процесса по значениям полюсов и нулей передаточной функции САУ.
Заметим, что при исследовании устойчивости нас интересовали лишь полюсы, здесь же необходимо учитывать и нули. Только в частном случае, когда нулей нет, качество переходного процесса определяется только полюсами. Начнем рассмотрение именно с такого случая.
Переходной процесс в устойчивой системе распадается на затухающие и колебательные составляющие. Если найти длительность самой длительной составляющей и величину колебательности самой колебательной составляющей, то по ним можно оценить верхние пределы величин длительности и колебательности всего переходного процесса.
Время затухания отдельной составляющей определяется величиной
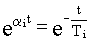
где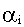 
- действительная часть i-го корня характеристического уравнения,
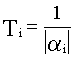- постоянная времени затухания.
Можно считать, что длительность i-ой составляющей переходного процесса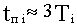 
, то есть длительность составляющих переходного процесса обратно пропорциональна абсолютному значению действительной части корней характеристического уравнения.
Абсолютная величина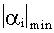 
называется степенью устойчивости и обозначается 
.
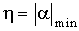При этом длительность переходного процесса будет
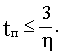
Термин “степень устойчивости” связан с тем, что геометрически 
- есть расстояние от мнимой оси, являющейся границей устойчивости, до ближайшего корня (см. рис.3.1).
Колебательность колебательной составляющей переходного процесса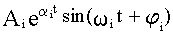 
определяется отношением соседних максимумов:
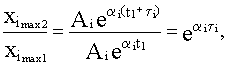
где t1- момент появления первого максимума i-й составляющей пере-
ходной характеристики,
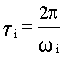- период колебаний данной составляющей.
Таким образом, колебательность равна
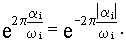
Следовательно, мерой колебательности является отношение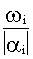 
: чем оно больше, тем больше колебательность составляющей. Наиболее колебательной является составляющая, у которой это отношение максимально. Соответствующая величина обозначается 
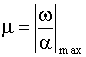и называется степенью колебательности.
В комплексной плоскости корень, определяющий наиболее колебательную составляющую, соответствует наибольшему значению угла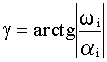 
между лучом, направленным через корень из начала координат, и действительной отрицательной полуосью.
Далее отметим влияние на качество переходного процесса наличия нулей передаточной функции. Положительные члены полинома числителя передаточной функции приведут к повышению колебательности и убыстрению переходного процесса, а отрицательные - к затягиванию переходного процесса.
Интегральными критериями качества называются такие, которые одним числом оценивают и величины отклонений, и время затухания переходного процесса. Для пояснения используем рис.4.9.
Рис.4.9
Обозначим отклонение выходной величины от нового установившегося значения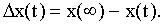 
Для монотонного процесса интегральной оценкой может служить заштрихованная площадь над кривой переходного процесса (см. рис.4.9), то есть
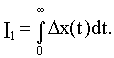
Интеграл I1 называется линейной интегральной оценкой. Процесс будет тем лучше, чем меньше число I1.
Однако такая оценка не годится для колебательного процесса, так как площади, расположенные ниже и выше прямой х(), будут иметь разные знаки. Поэтому по минимуму величины I1 наилучшим оказался бы процесс с незатухающими колебаниями.
В связи с этим в общем случае принимают квадратичную интегральную оценку качества в виде
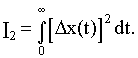
Целесообразность применения интегральных критериев заключается в том, что в литературе имеются формулы, выражающие I2 (или другие интегральные оценки) непосредственно через коэффициенты дифференциального уравнения САУ.
Интегральные критерии качества используются для определения оптимальных значений варьируемых параметров по минимуму значения соответствующей интегральной оценки.
Применяются интегральные критерии обычно в теории оптимальных систем.
К содержанию
4.3. Последовательная коррекция динамических свойств
Коррекция динамических свойств осуществляется с целью выполнения требований по устойчивости и качеству переходного процесса.
Осуществляется коррекция с помощью введения в САУ специальных корректирующих звеньев. Эти звенья могут включаться либо последовательно с основными звеньями САУ, либо параллельно им. Соответственно они и называются: последовательные либо параллельные корректирующие звенья.
Последовательные корректирующие звенья можно разделить на три типа: пропорционально-дифференцирующие (ПД), пропорционально-интегрирующие (ПИ) и пропорционально-интегро-дифференцирующие (ПИД) звенья.
ПД-звено имеет передаточную функцию
WПД(p)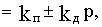
то есть выходная величина этого звена пропорциональна входной величине и ее первой производной.
Включение этого звена в САУ приводит к тому, что передаточная функция разомкнутого контура САУ
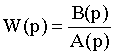
умножается на WПД(p), то есть принимает вид
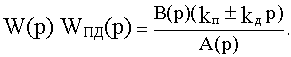
В результате характеристический полином замкнутой САУ D(р) будет следующий:
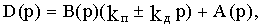
где A(p)=anpn+an-1pn-1+...+a1p+a0.
Положим, что В(р)=k (так как мы исследуем влияние ПД-звена, то логично предположить, что в исходной САУ такого звена не было, но тогда числитель передаточной функции исходной САУ содержит лишь величину k). Тогда можно видеть, что в характеристическом полиноме замкнутой САУ изменится коэффициент при р в первой степени. Включение двух ПД-звеньев приведет к изменению коэффициента и при p2 и т.д. Изменение же этих коэффициентов изменяет условия устойчивости и качество переходного процесса.
Рассмотрим в качестве примера применение данного звена для стабилизации, то есть обеспечения устойчивости САУ с астатизмом выше первого порядка (порядок астатизма - это число интегрирующих звеньев в приведенной одноконтурной САУ).
Передаточную функцию разомкнутой САУ с порядком астатизма, равным r, можно представить в виде:
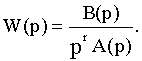
Соответственно характеристический полином замкнутой САУ будет:
D(р)=В(р)+prA(p).
Если В(р)=k, то из последнего выражения следует вывод о том, что САУ с порядком астатизма r>1 являются структурно неустойчивыми, поскольку в D(р) отсутствуют члены с р в степени от единицы до (r-1) (по критерию устойчивости Гурвица).
Введем теперь в систему (r-1) ПД-звеньев. При этом в харктеристическом полиноме появятся недостающие звенья:
D(p)=k(kп+kД1p+...+kД(r-1)pr-1)+prA(p).
Следовательно, САУ становится структурно устойчивой.
Влияние ПД-звена на качество переходного процесса продемонстрируем на примере последовательного соединения этого звена с апериодическим звеном с передаточной функцией
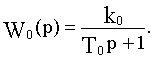
Передаточная функция последовательного соединения этих звеньев:
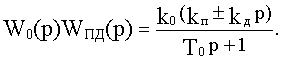
Соответственно переходная функция
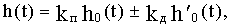
где h0(t)- переходная функция апериодического звена.
Из последнего выражения видно, что отрицательное дополнительное воздействие по производной снижает быстродействие, а положительное, наоборот, повышает его. Например, при kд/kп=T0 полностью компенсируется инерционность апериодического звена:
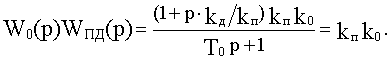
Реальные ПД-звенья обладают инерционностью, то есть имеют следующую передаточную функцию:
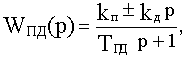
где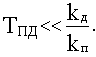 
Все сказанное выше об идеальном ПД-звене справедливо и для реального с той только разницей, что реальное слабее влияет на быстродействие и на области устойчивости.
ЛАЧХ реального ПД-звена приведена на рис.4.10.
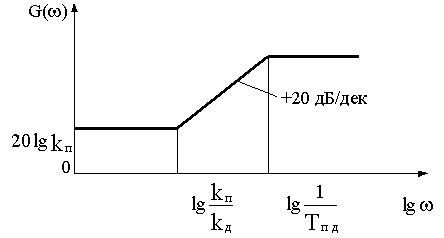
Рис.4.10
ПД-звено является фильтром верхних частот, так как его ЛАЧХ растет с увеличением частоты. Поэтому введение этого звена в САУ расширяет ее полосу пропускания, повышает быстродействие.
Практически наиболее просто ПД-звенья реализуются в электрических системах постоянного тока, где они представляют собой пассивные RC- и RL- цепочки. Один из возможных вариантов представлен на рис.2.4.
Пример реализации ПД-звена на операционном усилителе приведен на рис.4.11.
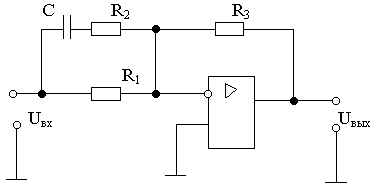
Рис.4.11
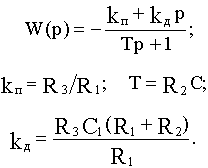
Пропорционально-интегрирующее (ПИ) звено имеет передаточную функцию
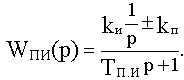
В случае ТПИ=0 получаем идеальное ПИ-звено.
Последнее выражение можно представить так:
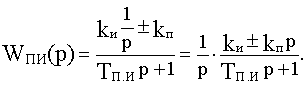
Таким образом, ПИ-звено эквивалентно последовательному соединению интегрирующего звена и ПД-звена. По своим частотным свойствам ПИ-звено противоположно ПД-звену, являясь фильтром нижних частот. ЛАЧХ ПИ-звена приведена на рис.4.12.
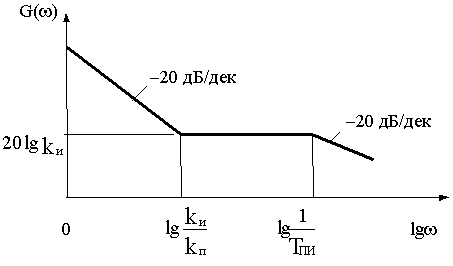
Рис. 4.12
Передаточная функция пропорционально-интегро-дифференциру-ющего (ПИД) звена
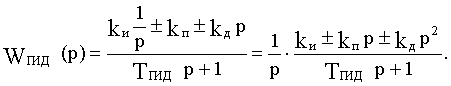
Это звено эквивалентно последовательному соединению интегрирующего звена и пропорционально-дифференцирующего с воздействием по двум производным или, что то же самое, последовательному соединению ПИ-звена и ПД-звена с одной производной. Таким образом, ПИД-звено повышает порядок астатизма, как и ПИ-звено, но при этом одновременно дает более сильную коррекцию динамических свойств САУ.
Такое звено подчеркивает как нижние, так и средние частоты, подавляя средние, как видно из приближенной ЛАЧХ ПИД-звена, приведенной на рис.4.12.
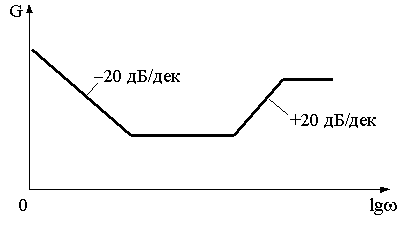
Рис.4.12
В связи с видом ЛАЧХ ПИД-звеньями называют не только звенья с указанной выше передаточной функцией Wпид(p), но и любые другие звенья, ЛАЧХ которых имеет минимум на средних частотах и растет в сторону как низких, так и высоких частот.
Вообще указанные выше наименования типов последовательных корректирующих звеньев в значительной степени условны прежде всего из-за инерционности реальных корректирующих звеньев.
Наиболее просто синтез последовательного корректирующего устройства можно произвести по ЛАЧХ. Для этого необходимо использовать ЛАЧХ нескорректированной САУ Gнескорр() и желаемую ЛАЧХ, Gскорр() соответствующую заданному переходному процессу. ЛАЧХ Gскорр() получают с помощью частотного критерия качества, иллюстрированного приведенными выше графиками (см. рис.4.7, рис.4.8).
При последовательном соединении звеньев справедливо соотношение
Wскорр(р)= Wнескорр(р)Wку(р),
где Wку(р) - передаточная функция синтезируемого последовательного корректирующего устройства.
Следовательно
Wку(р)=Wскорр(р)/Wнескорр(р).
Перейдем к частотной форме записи, используя логарифмические единицы:
20lg |Wку(р)(
)|=20lg |Wcкорр.()|- 20lg |Wнескорр.()|;
Gку()=Gскорр.() - Gнескорр.().
Тип и параметры последовательного корректирующего устройства получают следующим образом:
1) графически вычитают из желаемой ЛАЧХ ординаты ЛАЧХ исходной системы;
2) упрощают ЛАЧХ корректирующего устройства, сравнивают с ЛАЧХ имеющихся в справочных данных типовых корректирующих звеньев и выбирают конкретную схему корректирующего звена;
3) находят по сопрягающим частотам параметры схемы корректирующего устройства.
К содержанию
4.4. Параллельная коррекция
Параллельные корректирующие устройства реализуются в виде обратных связей. Корректирующие обратные связи (охватывающие отдельные звенья или участки цепи САУ) помимо классификации на отрицательные и положительные, делятся на жесткие и гибкие. Жесткие обратные связи осуществляются статическими звеньями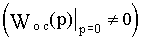 
, гибкие - дифференцирующими 
.
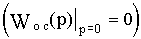Рассмотрим действие идеальной жесткой обратной связи с передаточной функцией Woc(p)=koc
Пусть эта обратная связь охватывает апериодическое звено с передаточной функцией
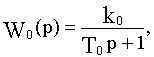
как показано на рис.4.13.
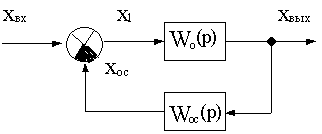
Рис.4.13
В результате охвата обратной связью получим
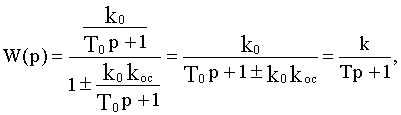
где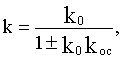 
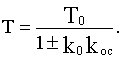
Постоянная времени и коэффициент передачи уменьшаются при отрицательной обратной связи и увеличиваются при положительной. На рис.4.14 иллюстрируется физическая суть механизма уменьшения инерционности при отрицательной обратной связи.
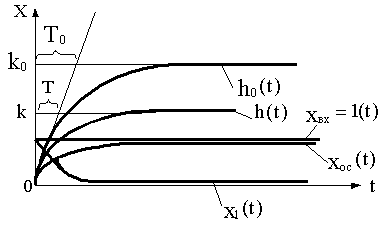
Рис.4.14
Переходная характеристика h0(t) соответствует апериодическому звену без обратной связи, а характеристика h(t)- с обратной связью.
Кривая сигнала x1(t)=1(t)-xoc(t) на входе звена имеет всплеск вначале. За счет его происходит форсировка на входе по сравнению с окончательным установившимся значением x1, которая и дает ускорение переходного процесса.
При инерционности обратной связи скорость роста xoc еще более замедлится, увеличится длительность форсировки на входе звена, в результате чего еще более повысится быстродействие.
В качестве жесткой корректирующей обратной связи применяется в основном отрицательная обратная связь для уменьшения инерционности.
Заметим попутно, что отрицательная обратная связь имеет и другие достоинства: она уменьшает остающуюся вне рассмотрения нелинейность статической характеристики звена, нестабильность его параметров во времени, а также при наличии шумов (помех) на входе или внутри звена уменьшает уровень шумов на выходе.
При охвате жесткой обратной связью интегрирующего звена с
W0(p)=k0/p имеем:
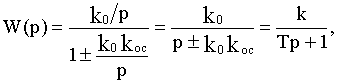
где
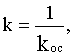
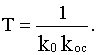
Таким образом интегрирующее звено превращается в статическое. Практический интерес при этом представляет лишь отрицательная связь (при положительной звено получается неустойчивым).
Рассмотрим далее влияние безинерционной гибкой обратной связи с Woc(p)=kocp, называемой еще гибкой обратной связью по скорости.
В общем случае для звена с передаточной функцией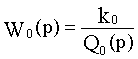 
имеем:
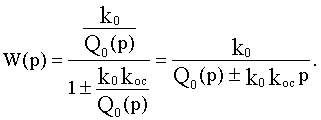
Таким образом гибкая обратная связь, не влияя на коэффициент передачи охватываемого звена, изменяет коэффициент при р в знаменателе передаточной функции.
В случае апериодического звена изменится постоянная времени (при положительной обратной связи уменьшится, а при отрицательной - возрастет), в случае колебательного - изменится коэффициент демпфирования.
